process used to estimate an unknown value between two known values by utilizing a common mathematical relation (e.g., proportion, function, linear, or logarithmic). Interpolation is commonly needed when consulting present value tables in which a present value interest factor is desired for a given period and unlisted interest rate. One would use the two closest listed interest rates, above and below the given interest rate, to estimate the present value factor needed for a given computation. Interpolation is more than likely used to find the Internal Rate of Return (IRR) on an investment project.
To illustrate the process of interpolation, let us assume that the investment required is $6000, the annual cost savings is $1000, and the life of the project is 10 years. The internal return can be determined as follows:The relevant factor is investment required/annual cost savings =$6000/$1000 = 6.000.
Looking at the present value of an annuity of $1.00 (see table 4 in back of book) and scanning along the 10-period line, we find a factor of 6.000 will yield a rate of return between 10% and 12%. To find the rate, use the interpolation as follows:
| Rate | Present Value Factor | |
| 10% | 6.145 | 6.145 |
| True rate | 6.000 | |
| 12% | 5.650 | |
| Difference | 0.145 | 0.495 |
estimation of an unknown number intermediate between known numbers. For instance, interpolation is a way of approximating price or yield using tables that do not give every possible answer.
- in mathematics, the process of estimating an unknown value of a function in between two known values. For example, if it takes 18 minutes to cook a 1-inch-thick steak and 40 minutes to cook a 2-inch steak, you can interpolate and find that it should take about 30 minutes to cook a 1½ -inch steak.
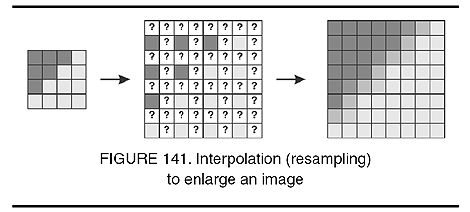
- in computer graphics, the process of smoothing the pixels in an image that has been enlarged by filling in intermediate colors or shades of gray, thus reducing the stairstep appearance that would otherwise result from enlarging a small bitmap; also known as resampling. See resample.
estimation of an unknown number intermediate between known numbers. Interpolation is a way of approximating price or yield using bond tables that do not give the net yield on every amount invested at every rate of interest and for every maturity. Interpolation is based on the assumption that a certain percentage change in yield will result in the same percentage change in price. The assumption is not altogether correct, but the variance is small enough to ignore.
| Therefore, the internal rate of return |
| = 10% + (0.145/0.495)(12% - 10%) |
| = 10% + 0.29 (2%) = 10% + 0.58% = 10.58% |